Parameters and calibrations
Here we present the parameters to be determined in order to carry out the calibration.
Reference measure outside the atmosphere
Determination of`N_0`
If a solar photometer sees the Sun through the different values of the relative mass of the air and the total atmospheric optical thickness does not change then the logarithm of the measurement is proportional to the relative mass of the air. By fitting a line through the data (a linear regression), the intersection of this line with the y-axis, where m = 0 is the logarithm of the measure that the instrument would produce if there were no atmosphere. This is called a "Langley" graphic calibration, named after Samuel P. Langley, the scientist who developed this technique in the early 20th century. (This work is described by Abbott and Fowle [1908], as part of early efforts in the early 20th century to determine "the solar constant of radiation.").
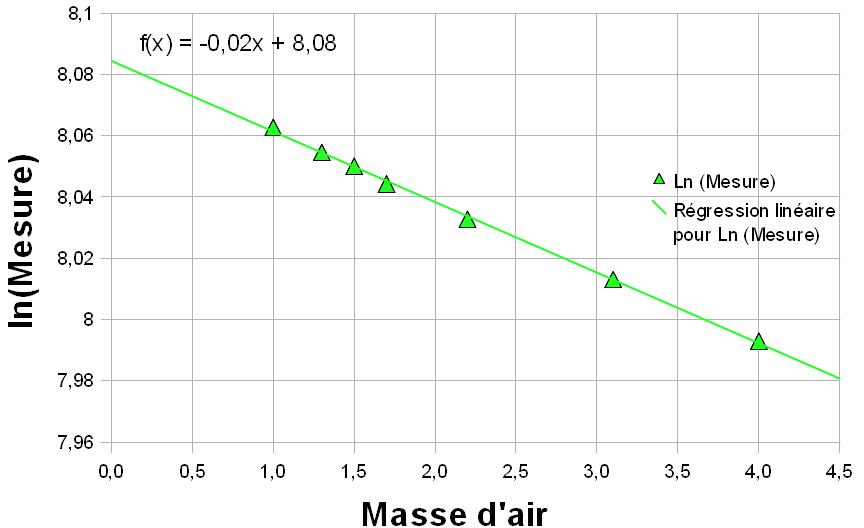
Simulation of measurements performed on June 21 [Based on data published by Brooks and Mims in 2000]
The logarithm of the measurement at m = 0 is 8.08. This gives a measure of 3229. Measure No should be normalized at an average distance of Earth-Sun (1 AU). On June 21, the distance Earth-Sun was 1.01631 UA. (It is true that in the northern hemisphere, the Earth is further away from the sun in summer). The intensity of the Sun's radiation, and thus the measurement, varies as the square of the Earth-Sun distance, so that :
No = (3229) (1,01631)² = 3335
If the instrument was at 1 AU of the Sun, the measure would be more important than it was on 21 June.
The solar photometers used in this frame can be calibrated by comparison in pairs, using a reference instrument for which a Langley graphic calibration was performed. This is called intercalibration.
Rayleigh coefficient
`a_R` determined from the spectral responses of the sensor
According to the American Meteorological Society document, in 1994, Dutton proposed the following formula valid only in the visible spectrum:
`tau_r = a_R * p / p_0`
`tau_r = 0.00877 * lambda^[-4,05] * p / p_0`
For the CALITOO, light wavelengths used are :
| wavelength (μm) | aR calculated |
| 0.465 | 0.19490 |
| 0.540 | 0.10637 |
| 0.619 | 0.06119 |
Ozone coefficients
`tau_[O_3]` as a function of the wavelength of the light is given by the LOA :
`tau_[O_3]"blue" = 0.0 `
`tau_[O_3]"green" = 0.0128`
`tau_[O_3]"red" = 0.0154`






